In mathematics, particularly in the realms of geometry and number theory, lattice points hold significant importance. They are fundamental elements in understanding the structure and properties of lattices, which have applications across various fields such as crystallography, cryptography, and computer graphics. In this article, we will delve into the definition of lattice points, explore related concepts, and discuss their significance in different areas of study.
Definition of Lattice Points:
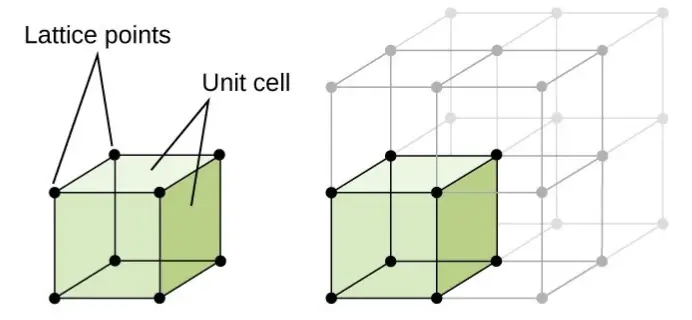
Lattice points are points in space with integer coordinates. More formally, in two-dimensional Euclidean space, a lattice point is a point with coordinates (x, y), where both x and y are integers. In three-dimensional space, lattice points are represented by coordinates (x, y, z), where x, y, and z are integers. This concept can be extended to higher dimensions as well.
Visually, lattice points form a grid-like structure, resembling the lattice framework commonly seen in windows or fences. Each lattice point is typically represented by a dot on a coordinate plane, and the collection of all lattice points creates a lattice.
Characteristics of Lattice Points:
- Integer Coordinates: As mentioned earlier, lattice points have coordinates consisting of integers. This characteristic distinguishes them from other points in space, which may have non-integer coordinates.
- Regular Arrangement: Lattice points are regularly spaced, forming a uniform grid pattern. The distance between adjacent lattice points remains constant and equal along each axis.
- Infinite in Number: Lattice points extend infinitely in all directions. There is no limit to the number of lattice points that can be generated within a lattice structure.
Related Concepts:
- Lattice: A lattice is a discrete set of points in space arranged in a regular, periodic pattern. Lattices are often classified based on their symmetry properties, such as square lattices, hexagonal lattices, and cubic lattices.
- Unit Cell: In crystallography, a unit cell is the smallest repeating unit within a crystal lattice that retains the overall symmetry of the lattice. It is defined by its lattice parameters, which specify the lengths of the edges and the angles between them.
- Basis: In the context of lattices, a basis is a set of vectors that define the arrangement of points within the lattice. By combining the basis vectors with integer coefficients, any lattice point within the structure can be expressed.
- Primitive Cell: The primitive cell of a lattice is the smallest unit cell that contains exactly one lattice point. It is a fundamental building block for constructing the entire lattice structure.
- Bravais Lattice: A Bravais lattice is a specific type of lattice characterized by its translational symmetry. There are 14 possible Bravais lattices in three-dimensional space, classified based on their lattice geometry and symmetry properties.
Significance of Lattice Points:
- Crystallography: In crystallography, lattice points play a crucial role in describing the arrangement of atoms within crystalline materials. The lattice structure determines various properties of crystals, including their symmetry, diffraction patterns, and mechanical behaviour.
- Cryptography: Lattices are utilized in cryptography for constructing cryptographic systems with strong security properties. Lattice-based cryptography relies on the difficulty of certain lattice problems, such as the shortest vector problem, for ensuring the security of cryptographic protocols.
- Computer Graphics: Lattice points are employed in computer graphics for representing and manipulating geometric shapes. They serve as the basis for various rendering techniques, such as texture mapping, surface subdivision, and ray tracing.
- Number Theory: Lattice points are studied in number theory for their connections to Diophantine equations and integer programming problems. Techniques from lattice theory are applied to analyse and solve mathematical problems involving integer solutions.
In conclusion, lattice points are fundamental elements in mathematics with diverse applications across various disciplines. Their regular arrangement and integer coordinates make them indispensable for understanding the structure and properties of lattices, paving the way for advancements in fields ranging from crystallography to cryptography.