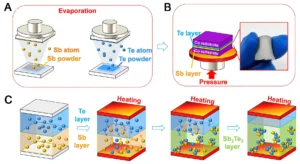
Surface tension is a captivating phenomenon in physics that manifests at the interface of liquids and solids, defining the behaviour of liquid surfaces. This phenomenon arises due to the cohesive forces between molecules at the surface of a liquid, leading to unique properties and behaviours that have significant implications in various scientific and everyday applications.
Understanding Surface Tension:
Surface tension is the result of the attractive forces between molecules at the surface of a liquid. These forces arise from intermolecular interactions, such as van der Waals forces and hydrogen bonding, which tend to pull the molecules on the surface inward. As a result, the surface of a liquid behaves like a stretched elastic membrane, resisting any force that tries to increase its surface area.
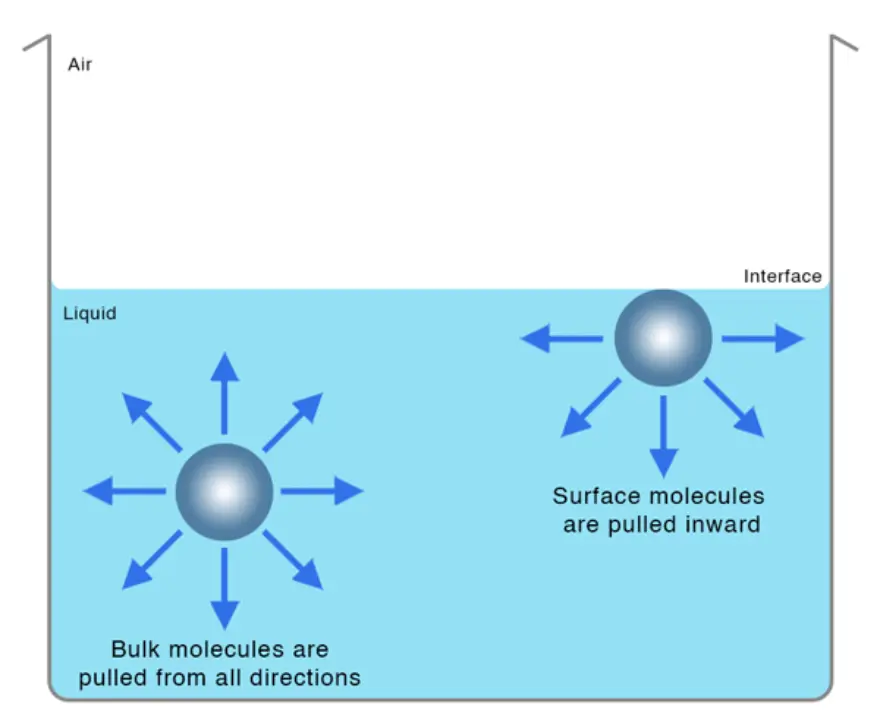
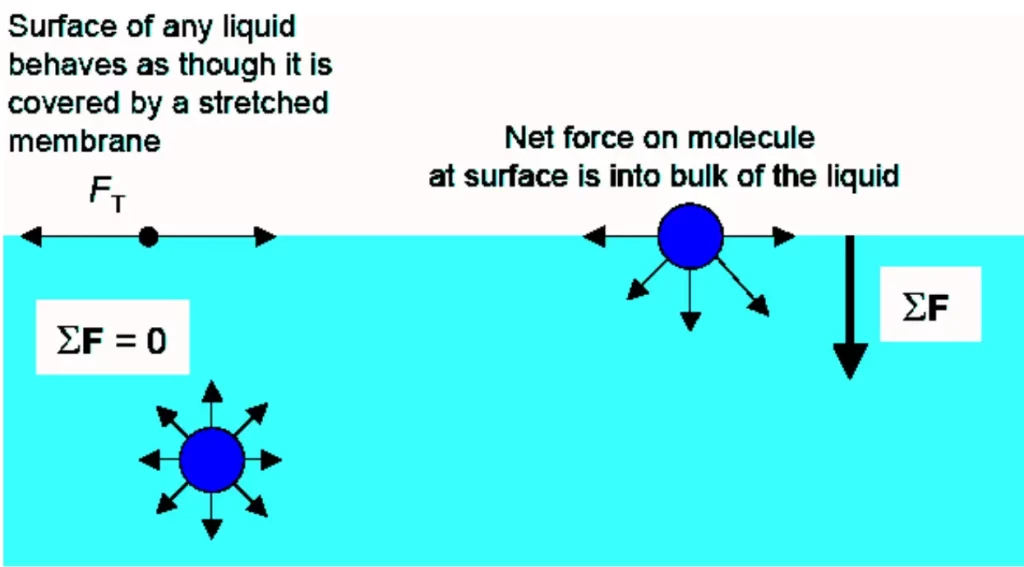

Mathematically, surface tension (T) can be defined as the force acting perpendicular to a line of unit length on the liquid surface. It is measured in units of force per unit length, typically in newtons per meter (N/m).
Capillary Action:
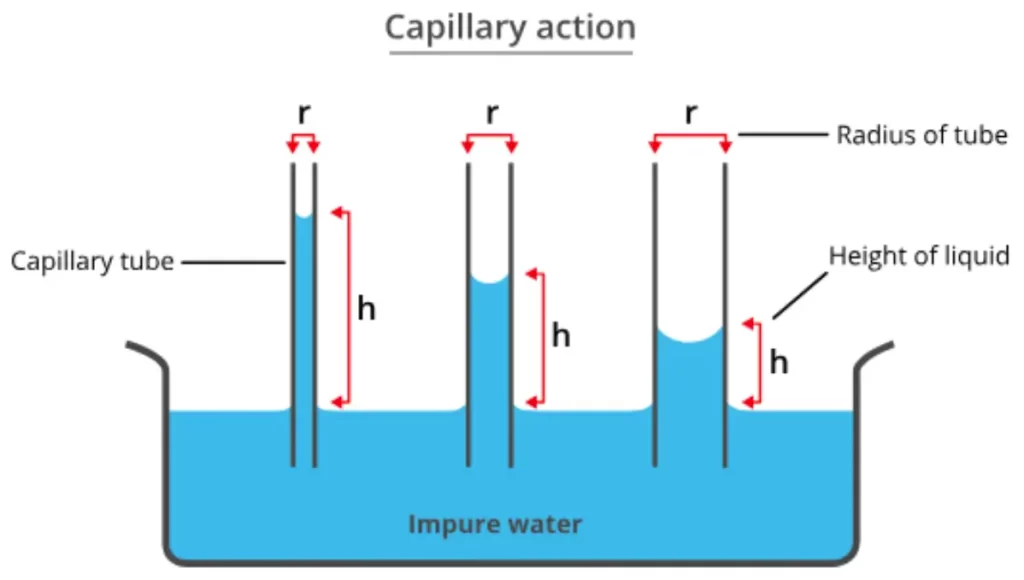
One of the most intriguing consequences of surface tension is capillary action. When a narrow tube (capillary) is inserted into a liquid, the liquid level within the tube deviates from the surrounding liquid level. This is due to the balance between adhesive forces (attraction between liquid molecules and tube walls) and cohesive forces (attraction between liquid molecules). Capillary action has applications in phenomena like water absorption in plants and the operation of capillary tubes in medical devices.
Formation of Drops and Bubbles:
Surface tension also plays a crucial role in the formation of drops and bubbles. When a liquid is dispensed from a nozzle, surface tension causes the liquid to form droplets. Similarly, when a gas is trapped within a liquid, surface tension tends to minimise the surface area, resulting in the formation of bubbles. Understanding these phenomena is vital in various industrial processes, from inkjet printing to the production of pharmaceuticals.
Young-Laplace Equation:
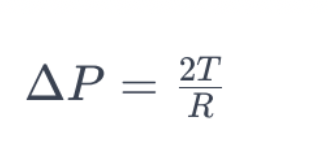
The Young-Laplace equation is a fundamental concept related to surface tension, providing insights into the pressure difference across a curved liquid interface. The equation relates the pressure difference (ΔP), radius of curvature (R), and surface tension (T) for a curved interface.
Applications in Nature and Industry:
Surface tension has diverse applications in both natural and industrial settings. In nature, it influences the behaviour of water striders gliding effortlessly on the water’s surface and the coalescence of raindrops in the atmosphere. In industry, it is exploited in processes such as emulsification, where surface tension helps mix immiscible liquids like oil and water.
Conclusion:
Surface tension is a captivating and versatile phenomenon in physics, governing the behaviour of liquid surfaces and influencing various natural and industrial processes. Its study not only enhances our understanding of fundamental physics but also contributes to the development of technologies and applications that impact our daily lives. As researchers continue to delve into the intricacies of surface tension, new discoveries and innovations are likely to emerge, further expanding our knowledge of this fascinating aspect of physics.