In the realm of physics, equilibrium is a fundamental concept that describes the state of an object when it experiences no net force or torque.
Understanding different types of equilibrium:
- Stable,
- Unstable,
- Neutral
They are crucial in various fields, from mechanics to engineering. These concepts help us predict the behaviour of objects under different conditions and design structures that remain stable in their environments.
1. Stable Equilibrium:
Stable equilibrium refers to a condition in which an object, when displaced from its original position, experiences a restoring force or torque that brings it back to its initial state.
Examples:
- A ball sitting at the bottom of a bowl. If you perturb the ball slightly, gravity pulls it back towards the centre, stabilising its position.
- Imagine a simple pendulum: a mass attached to a string suspended from a fixed point. When the pendulum is at rest, hanging vertically downward, it’s in stable equilibrium. If you displace it slightly to one side, gravity acts as a restoring force, pulling it back to its original position.
- Another example is a marble placed in a concave depression on a flat surface. Even if you nudge the marble, it rolls back to the bottom of the depression due to the force of gravity, demonstrating stable equilibrium.
In stable equilibrium, small disturbances from the equilibrium position lead to forces or torques that tend to oppose the displacement, restoring the object to its original position. Mathematically, stable equilibrium is characterized by the condition that the second derivative of the potential energy function with respect to the generalised coordinate (position) is positive. This condition ensures that the potential energy has a minimum at the equilibrium point. Mathematically, for a one-dimensional system, the condition for stable equilibrium can be expressed as:

In the case of multi-dimensional systems, the condition involves the second derivative of the potential energy with respect to each coordinate. All eigenvalues of the Hessian matrix of second derivatives must be positive for stable equilibrium.
2. Unstable Equilibrium:
Unstable equilibrium occurs when a small displacement from the equilibrium position results in a net force or torque that moves the object further away from its original position.
Examples:
- Picture a ball perched at the top of a hill. Any slight disturbance will cause it to roll down, away from its initial position, accelerating as it goes.
- Consider the case of a pencil balanced on its tip. While it may seem balanced momentarily, the slightest deviation from the vertical position will cause it to topple over, moving away from equilibrium rather than returning to it.
- Another example is an inverted pendulum: a pendulum balanced upside-down. If displaced slightly from its vertical position, gravity pulls it further away from equilibrium, leading to increasing displacement.
In unstable equilibrium, any disturbance leads to a net force or torque that amplifies the displacement, pushing the object further away from its original position.
Mathematically, this is characterized by the condition that the second derivative of the potential energy function with respect to the generalised coordinate is negative, indicating a maximum in potential energy at the equilibrium point.
For a one-dimensional system, the condition for unstable equilibrium can be expressed as:

In multi-dimensional systems, the eigenvalues of the Hessian matrix of second derivatives will include at least one negative eigenvalue for unstable equilibrium.
3. Neutral Equilibrium:
Neutral equilibrium describes a state where an object remains in equilibrium regardless of its displacement. This means that any displacement neither results in a restoring force or torque nor leads to further displacement.
Examples:
A common example is a ball resting on a flat, level surface. Regardless of its position on the surface, it remains at rest without any tendency to return to a specific point.
Neutral equilibrium can also be observed in certain symmetric configurations. For instance, a perfectly balanced seesaw with equal weights on both sides remains level regardless of the distribution of weight.
Mathematically, this is characterized by the condition that the second derivative of the potential energy function with respect to the generalised coordinate is zero, indicating a point of inflection in the potential energy curve at the equilibrium point.
For a one-dimensional system, the condition for neutral equilibrium can be expressed as:
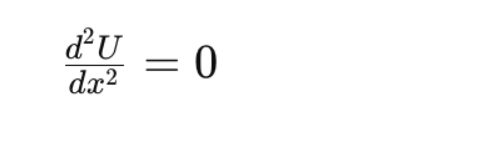
In multi-dimensional systems, the Hessian matrix of second derivatives will have at least one zero eigenvalue for neutral equilibrium.
Applications:
- Mechanics: These mathematical conditions are used to analyse the stability of mechanical systems such as pendulums, springs, and beams.
- Electromagnetism: Similar principles are applied to understand the stability of charged particles in electric and magnetic fields.
- Quantum Mechanics: Concepts of stability and equilibrium play a role in understanding the behaviour of quantum systems in potential wells.
- Engineering: Engineers use these concepts to design stable structures such as buildings, bridges, and vehicles that can withstand external forces and remain in equilibrium under different conditions.
In summary, stable, unstable, and neutral equilibrium in physics have distinct mathematical conditions involving the second derivative of the potential energy function with respect to the generalised coordinates. These conditions help predict the behaviour of systems and are foundational in various branches of physics and engineering.