Refraction, the bending of light as it passes from one medium to another, is a fundamental principle in optics. Refractive index is a crucial concept in understanding this phenomenon. It quantifies how much light is bent when passing from one medium to another. In this article, we will delve into the definition, formula, underlying concepts, examples, and applications of refractive index.
Definition
Refractive index, symbolized by 𝑛, is a dimensionless quantity that describes the speed of light in a medium relative to its speed in a vacuum. It indicates how much the direction of light is altered when it enters a different medium. Mathematically, it is expressed as the ratio of the speed of light in a vacuum (𝑐) to the speed of light in the medium (𝑣):
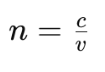
The formula for calculating refractive index is straightforward. Given the speed of light in a vacuum (𝑐) and the speed of light in a medium (𝑣), the refractive index (𝑛) can be calculated using the formula.
Detailed Concepts
Snell’s Law: Refraction is governed by Snell’s Law, which relates the angles of incidence and refraction to the refractive indices of the two media involved. It is mathematically expressed as:
𝑛1 × sin (𝜃1)= 𝑛2 × sin(𝜃2)
Where, 𝑛1 and 𝑛2 are the refractive indices of the first and second media respectively, and 𝜃1 and 𝜃2 are the angles of incidence and refraction.
Dependence on Wavelength: Refractive index can vary with the wavelength of light, a phenomenon known as dispersion. Different wavelengths of light experience different degrees of bending when passing through a medium, leading to effects like chromatic aberration in lenses.
Temperature and Pressure Dependence: Refractive index can also be influenced by factors such as temperature and pressure. Changes in these parameters can alter the density of the medium, affecting the speed of light and consequently, the refractive index.
Examples
- Air to Glass Transition: Consider light traveling from air (refractive index approximately 1) to glass (typical refractive index around 1.5). As light enters the glass, it slows down, causing it to bend towards the normal.
- Water to Air Transition: When light travels from water (refractive index approximately 1.33) to air, it speeds up, leading to less bending away from the normal.
- Diamond’s High Refractive Index: Diamond has an exceptionally high refractive index of around 2.42, which contributes to its brilliance and optical properties, making it desirable for use in jewellery.
Applications
- Optical Fiber Communications: Understanding refractive index is essential for designing and optimising optical fibre communication systems. The refractive index of the fibre core relative to the cladding determines the critical angle for total internal reflection, enabling light to be efficiently transmitted through the fibre.
- Lens Design: Refractive index plays a crucial role in lens design for optical instruments like cameras and microscopes. Different lens materials with varying refractive indices are used to control properties such as aberrations and focal length.
- Medical Imaging: In medical imaging techniques like microscopy and endoscopy, refractive index matching is employed to minimise distortions and maximise image clarity by reducing reflections at interfaces.
- Material Characterisation: Refractive index measurements are utilized in material characterisation techniques such as ellipsometry, which is used to determine properties like film thickness and optical constants of thin films.
- Gemology: Gemologists use refractive index measurements as a diagnostic tool to identify gemstones. Each gemstone has a unique refractive index, aiding in their identification and authentication.
Conclusion
Refractive index is a fundamental concept in optics with widespread applications across various fields including telecommunications, lens design, medical imaging, material science, and gemology. Understanding its definition, formula, underlying concepts, examples, and applications provides a solid foundation for exploring and utilizing the principles of light propagation in different mediums.