Statistical Mechanics serves as a cornerstone in the field of physics, providing a bridge between the microscopic realm of individual particles and the macroscopic properties of materials we observe in our everyday lives. At the heart of this theoretical framework lies the concept of ensembles, which plays a pivotal role in understanding the behaviour of large systems governed by statistical laws. Ensembles provide a powerful tool for physicists to explore and predict the properties of matter, shedding light on the inherent uncertainties and fluctuations that characterise the microscopic world.
Ensemble Theory:
In statistical mechanics, an ensemble refers to a collection of possible microscopic states that a system could occupy, each with a certain probability. This approach allows physicists to study the statistical behaviour of a system rather than tracking the exact evolution of each individual particle. There are several types of ensembles, each with its unique set of characteristics and applications. The most fundamental ones are the micro-canonical ensemble, canonical ensemble, and grand canonical ensemble.
1. Microcanonical Ensemble:
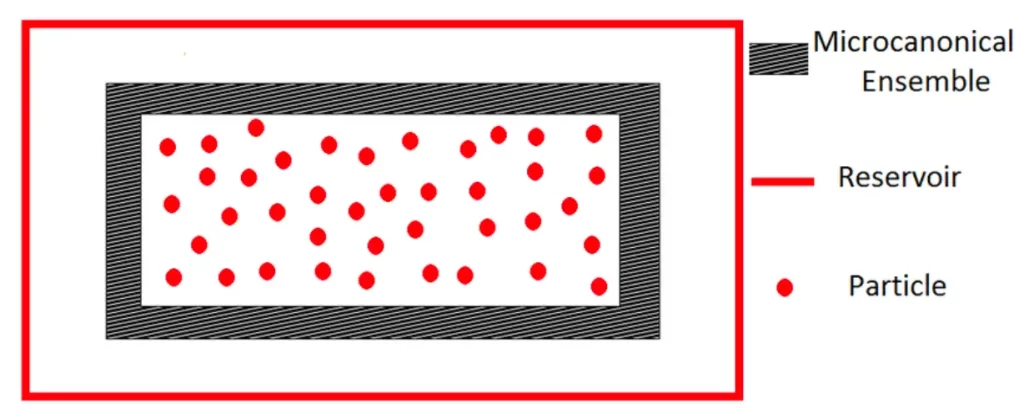
The microcanonical ensemble describes an isolated system with fixed energy, volume, and particle number. In this ensemble, all accessible microstates are equally probable. Physicists use this ensemble to investigate the fundamental principles of statistical mechanics, exploring concepts such as entropy, temperature, and the Boltzmann distribution.
2. Canonical Ensemble:
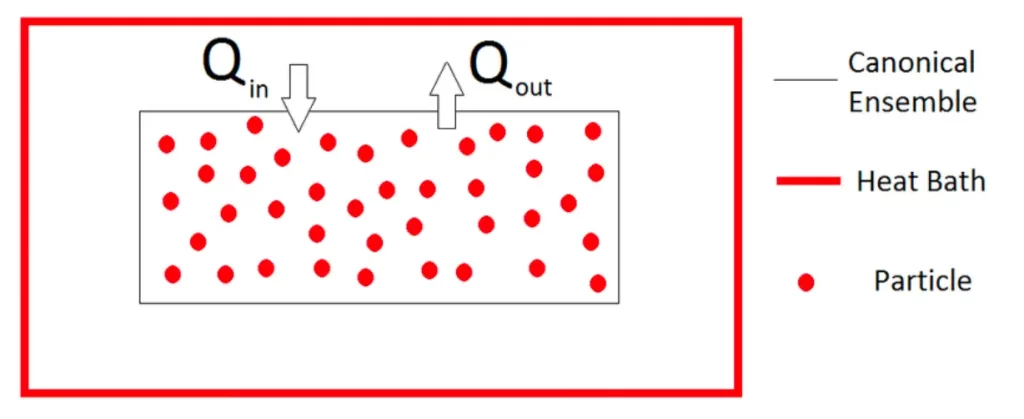
The canonical ensemble deals with systems that can exchange energy with a reservoir at a fixed temperature. In this ensemble, the energy is no longer fixed, but the temperature remains constant. The canonical ensemble is particularly useful in describing systems in thermal equilibrium with a larger heat bath, such as gases at a constant temperature.
3. Grand Canonical Ensemble:
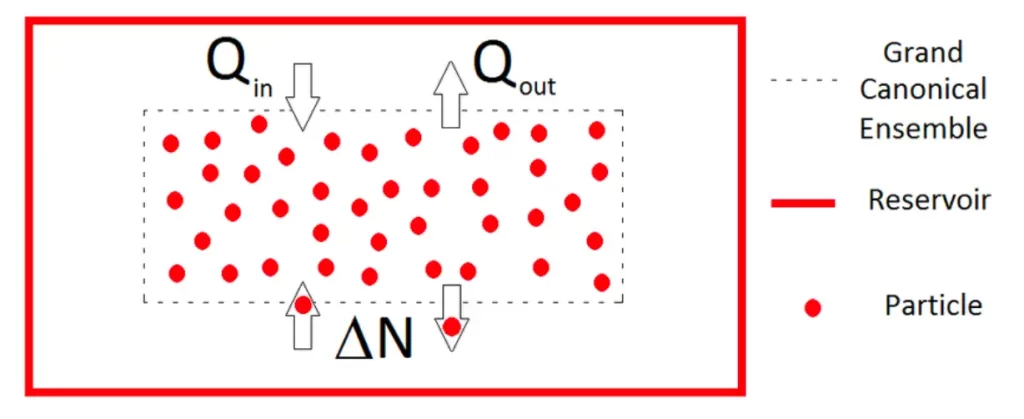
For systems in contact with a reservoir allowing both energy and particle exchange, the grand canonical ensemble comes into play. This ensemble is crucial for understanding systems at constant chemical potential, making it suitable for studying phase transitions involving changes in particle numbers, such as condensation or evaporation of gases.
Ensemble Averages and Thermodynamic Quantities:
Ensembles provide a framework for calculating averages and thermodynamic quantities, allowing physicists to make predictions about the macroscopic behaviour of a system. Key concepts include the partition function, which encapsulates information about the system’s energy states, and the Helmholtz free energy, a thermodynamic potential that becomes particularly useful in the canonical ensemble.
Applications in Condensed Matter Physics:
Ensemble theory finds extensive applications in condensed matter physics, where the behaviour of matter in bulk is of paramount importance. By employing ensembles, physicists can analyse phase transitions, investigate the properties of solids, liquids, and gases, and gain insights into the thermodynamics of complex materials.
Conclusion:
Ensemble theory in statistical mechanics provides a powerful and elegant framework for understanding the behaviour of large systems composed of countless microscopic particles. Through the exploration of different ensembles, physicists can unravel the mysteries of the microscopic world, predicting and explaining the macroscopic properties of matter. As technology advances and our understanding of statistical mechanics deepens, ensembles continue to be a cornerstone in the pursuit of unlocking the secrets of the physical universe.