Classical mechanics and quantum mechanics are two fundamental theories that describe the behaviour of physical systems at different scales. Classical mechanics, developed by physicists like Isaac Newton and later refined by others, is a deterministic theory that works well for macroscopic objects. On the other hand, quantum mechanics, developed in the early 20th century by pioneers such as Max Planck and Erwin Schrödinger, is a probabilistic theory that governs the behaviour of particles at the atomic and subatomic levels. This article explores the key differences between classical and quantum mechanics, highlighting their principles, applications, and implications.
Basic Principles:
Classical Mechanics:
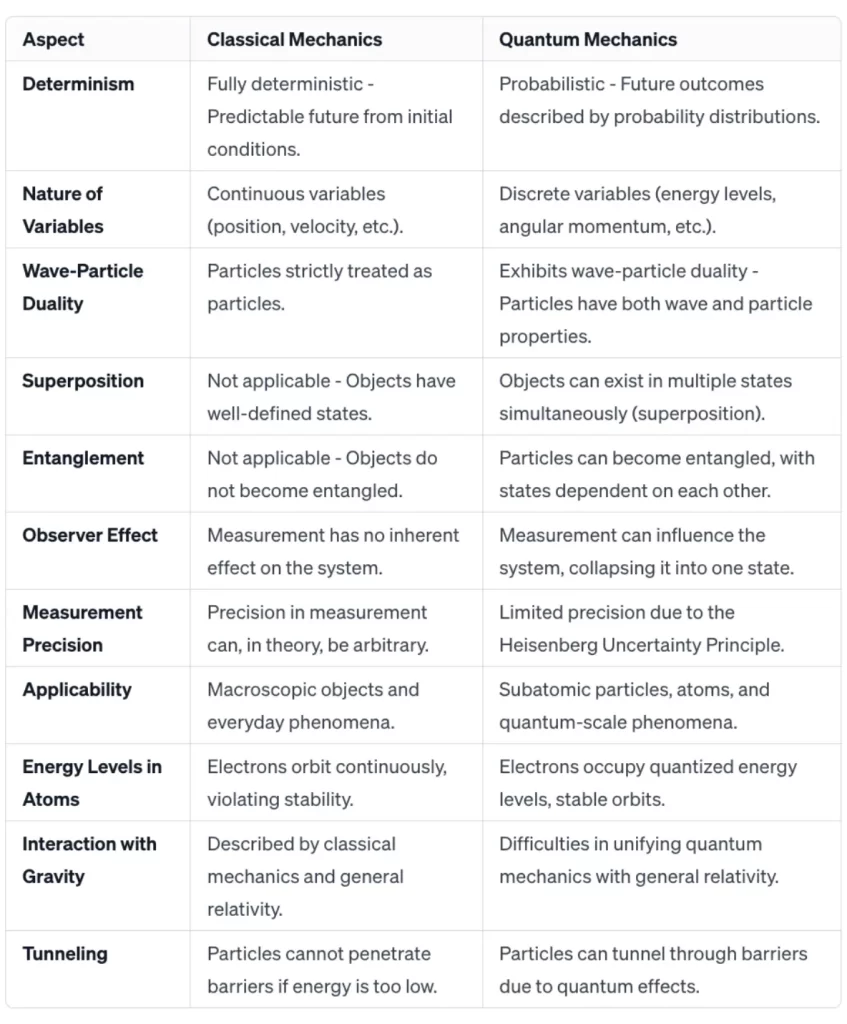
Determinism: Classical mechanics is based on the principle of determinism, meaning that the future behaviour of a system can be precisely predicted if the initial conditions are known.
Continuous Variables: Classical mechanics deals with continuous variables such as position, velocity, and acceleration.
Quantum Mechanics:
Probabilistic Nature: Quantum mechanics introduces a fundamental element of uncertainty. It describes the behaviour of particles in terms of probabilities, and it is impossible to predict the exact outcome of a measurement.
Discrete Variables: Quantum mechanics deals with discrete variables, such as energy levels and angular momentum, which are quantised.
Wave-Particle Duality:
Classical Mechanics:
Particles are strictly treated as particles with definite positions and velocities.
Quantum Mechanics:
Wave-Particle Duality: Particles, such as electrons and photons, exhibit both wave-like and particle-like properties. This duality is a central concept in quantum mechanics.
Superposition and Entanglement:
Classical Mechanics:
Objects have well-defined states, and the superposition of states is not a characteristic of classical systems.
Quantum Mechanics:
Superposition: Quantum systems can exist in multiple states simultaneously, a phenomenon known as superposition.
Entanglement: Particles can become entangled, meaning the state of one particle is directly related to the state of another, regardless of the distance between them.
Measurement and Observer Effect:
Classical Mechanics:
Measurement has no inherent effect on the system being measured.
Quantum Mechanics:
Observer Effect: The act of measurement in quantum mechanics can influence the state of the system, collapsing it into one of the possible states.
Let’s explore a few specific examples that highlight the differences between classical and quantum mechanics:
Particle Behavior:
Classical Mechanics: Consider a billiard ball on a frictionless table. Its position and velocity can be precisely determined using classical mechanics, and its future trajectory can be predicted based on Newton’s laws.
Quantum Mechanics: Now, consider an electron. In the quantum realm, the electron doesn’t have a definite trajectory. Its position is described by a probability distribution, and only the likelihood of finding it in a particular region can be predicted.
Double-Slit Experiment:
Classical Mechanics: If you shine light through two slits onto a screen, you’ll see two bands of light on the screen corresponding to the two slits. Classical wave theory predicts an interference pattern.
Quantum Mechanics: When individual particles, such as electrons, are sent through the double slits one at a time, an interference pattern still emerges. This implies that each particle behaves like a wave, showing the wave-particle duality inherent in quantum mechanics.
Quantum Tunneling:
Classical Mechanics: According to classical mechanics, a particle cannot penetrate a barrier if its energy is lower than the potential energy of the barrier.
Quantum Mechanics: Quantum tunnelling allows particles to pass through barriers that classical mechanics would consider impenetrable. This phenomenon is crucial in explaining processes like nuclear fusion in stars.
Uncertainty Principle:
Classical Mechanics: In classical mechanics, the simultaneous measurement of position and momentum can be done with arbitrary precision.
Quantum Mechanics: The Heisenberg Uncertainty Principle states that the more precisely you know the position of a particle, the less precisely you can know its momentum, and vice versa. This introduces a fundamental limit to the precision of measurements in the quantum world.
Entanglement:
Classical Mechanics: Two objects can have independent states regardless of their separation.
Quantum Mechanics: Quantum entanglement involves two or more particles becoming correlated in such a way that the state of one particle instantly influences the state of the other, no matter the distance between them.
Energy Levels in Atoms:
Classical Mechanics: Electrons orbiting a nucleus in a classical sense would continuously emit radiation and spiral into the nucleus, violating classical laws of stability.
Quantum Mechanics: Electrons in atoms occupy quantised energy levels. They can jump between these levels by absorbing or emitting discrete amounts of energy, and their behaviour is described by wave functions.
These examples illustrate the profound differences between classical and quantum mechanics, showcasing the transition from a deterministic and continuous world to a probabilistic and discrete one as we delve into the microscopic scales of the quantum realm.
Applications:
Classical Mechanics:
Applicable to macroscopic objects, celestial mechanics, and everyday phenomena.
Quantum Mechanics:
Essential for understanding the behaviour of atoms, molecules, subatomic particles, and quantum technologies such as quantum computing.
Limitations and Challenges:
Classical Mechanics:
Breaks down at the quantum level and cannot accurately describe phenomena at that scale.
Quantum Mechanics:
Does not seamlessly integrate with general relativity, leading to challenges in describing gravitational interactions at quantum scales.
Conclusion:
In summary, classical mechanics and quantum mechanics represent two distinct yet interconnected frameworks for understanding the physical world. While classical mechanics provides a deterministic and intuitive description of macroscopic systems, quantum mechanics introduces probabilistic and counterintuitive aspects that govern the behaviour of particles at the quantum level. The coexistence of these theories poses ongoing challenges and fuels ongoing research in the quest for a unified theory that can seamlessly encompass both classical and quantum phenomena.