The simple harmonic oscillator (SHO) is a fundamental concept in physics that describes the behaviour of a system oscillating around a stable equilibrium position. It is a ubiquitous phenomenon found in various natural and engineered systems, ranging from pendulums and springs to electronic circuits. The beauty of the simple harmonic oscillator lies in its ability to model a wide array of oscillatory motions and its significance in understanding the dynamics of physical systems.
Simple harmonic oscillator Definition:
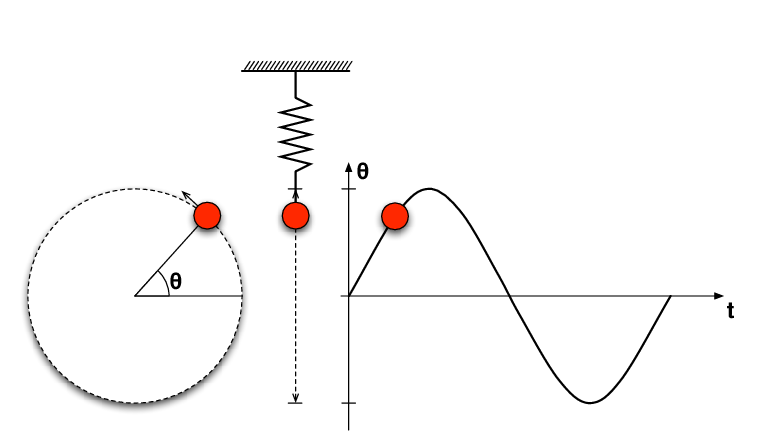
A simple harmonic oscillator is characterised by its motion, which is sinusoidal (or harmonic) in nature. The restoring force acting on the system is directly proportional to the displacement from the equilibrium position and is always directed towards that position. Mathematically, this relationship is described by Hooke’s Law:
F = −kx
Here, F is the restoring force, k is the spring constant (a measure of the stiffness of the system), and x is the displacement from the equilibrium position.
Equation of Motion:
The equation of motion for a simple harmonic oscillator can be derived using Newton’s second law, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Applying this law to a simple harmonic oscillator, we get the following second-order linear differential equation:

This equation illustrates that the energy is proportional to the square of the amplitude.
Applications:
- Mechanical Systems: Simple harmonic oscillators are prevalent in mechanical systems, such as mass-spring systems and pendulums, where their behaviour can be accurately modelled using the principles of SHO.
- Electrical Systems: Electrical circuits containing inductors, capacitors, and resistors can exhibit simple harmonic motion in the form of alternating currents and voltages.
- Quantum Mechanics: In quantum mechanics, the motion of electrons in a harmonic potential well is modelled as a simple harmonic oscillator.
- Acoustics: Vibrations in air molecules that create sound waves can be approximated as simple harmonic oscillations.
Conclusion:
The simple harmonic oscillator is a cornerstone in understanding the oscillatory behaviour of diverse systems across various scientific disciplines. Its elegant mathematical description and widespread applicability make it a fundamental concept in physics and engineering. The ability to comprehend and analyse simple harmonic motion provides valuable insights into the nature of vibrations and waves, enabling scientists and engineers to design and optimise systems across a broad spectrum of applications.