In the early 17th century, Johannes Kepler revolutionized our understanding of the cosmos by formulating three laws that describe the motion of planets around the Sun. Kepler’s Laws of Planetary Motion, derived from meticulous observations made by Tycho Brahe, laid the groundwork for modern astronomy and contributed significantly to the scientific revolution. Let’s explore the beauty and significance of Kepler’s laws in unraveling the mysteries of celestial orbits.
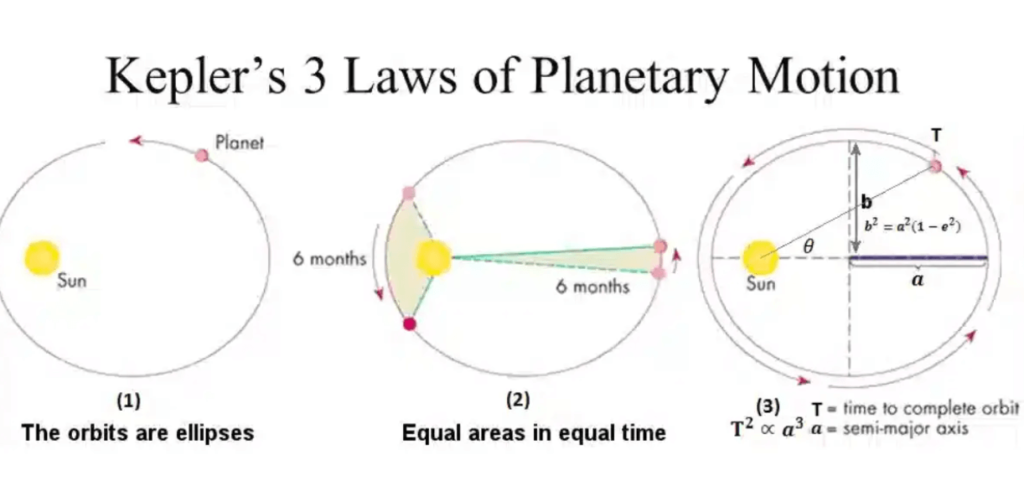
Kepler's First Law – The Law of Ellipses:
Kepler’s First Law states that the orbit of a planet around the Sun is an ellipse, with the Sun at one of the two foci. An ellipse is a geometric shape resembling a flattened circle, and the degree of flattening is quantified by its eccentricity. The closer an ellipse is to a perfect circle, the lower its eccentricity.
This law dispelled the long-held belief that planetary orbits were perfect circles, introducing a more accurate model for understanding celestial motion. The Sun’s position at one of the foci means that a planet’s distance from the Sun varies as it travels along its elliptical path.
Kepler's Second Law – The Law of Equal Areas:
Kepler’s Second Law, often referred to as the Law of Equal Areas, states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. In simpler terms, a planet travels faster in its orbit when it is closer to the Sun and slower when it is farther away.
This law is a consequence of the conservation of angular momentum. As a planet moves closer to the Sun, the gravitational force increases, causing the planet to accelerate. Conversely, as the planet moves farther away, the gravitational force weakens, leading to a decrease in speed. The cumulative effect is that the area swept out by the line segment connecting the planet and the Sun remains constant over time.
Kepler's Third Law – The Law of Harmonies:
Kepler’s Third Law relates the orbital period of a planet to its average distance from the Sun. It states that the square of the orbital period (T) of a planet is directly proportional to the cube of the semi-major axis (a) of its orbit. Mathematically, this can be expressed as T^2 ∝ a^3.
This law allows astronomers to compare the motions of different planets in our solar system. It means that planets farther from the Sun take longer to complete their orbits, and there is a predictable mathematical relationship between a planet’s distance and its orbital period.
Implications and Legacy:
Kepler’s laws not only provided a more accurate description of planetary motion but also laid the groundwork for Isaac Newton’s law of universal gravitation. Newton used Kepler’s laws to develop his theory of gravity, showcasing the interconnectedness of scientific discoveries.
The elegance of Kepler’s laws lies in their simplicity and their ability to explain the seemingly complex movements of celestial bodies. These laws are not limited to our solar system; they apply to any two-body system, whether it be a moon orbiting a planet or a binary star system.
Kepler’s Laws of Planetary Motion represent a pivotal moment in the history of astronomy, marking the transition from a geocentric to a heliocentric model of the solar system. Their enduring legacy continues to shape our understanding of the cosmos, guiding astronomers and physicists in their exploration of the universe. Kepler’s laws stand as a testament to the power of observation, mathematical insight, and the human capacity to unravel the mysteries of the cosmos.