In the realm of mathematics and physics, vectors are crucial for representing various physical quantities such as force, velocity, and displacement. One of the fundamental operations involving vectors is the dot product, also known as the scalar product. It holds significant importance in both theoretical formulations and practical applications across various fields of science and engineering.
Definition:
The dot product of two vectors is a scalar quantity that measures the projection of one vector onto another. It calculates the magnitude of one vector in the direction of another vector. Mathematically, if we have two vectors A and B, the dot product (denoted by · or sometimes by ⋅) is represented as:
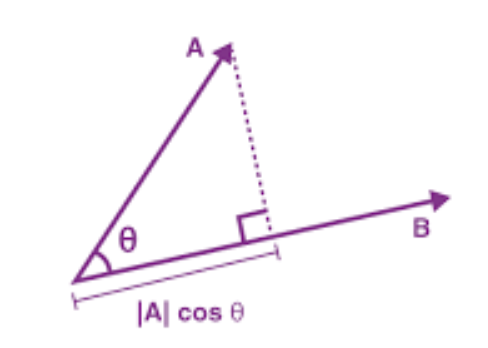
Dot product: A ⋅ B = ∣A∣ ∣B∣ cos(θ)
Where:
- ∣𝐴∣ and ∣B| are the magnitudes (lengths) of vectors A and B respectively.
- θ is the angle between the two vectors.

Characteristics:
- Commutativity: The dot product is commutative, meaning 𝐴 ⋅ 𝐵 = 𝐵 ⋅ 𝐴
- Scalar Result: The result of a dot product is a scalar, not a vector.
- Angle Between Vectors: The dot product is maximum when the vectors are parallel (𝜃 = 00), and minimum (zero) when perpendicular (𝜃 = 900)
- Zero Dot Product: Two vectors are perpendicular if and only if their dot product is zero.
Examples:
- Work Done: In physics, when a force 𝐹 acts on an object and displaces it by a vector 𝑑, the work done 𝑊 is given by the dot product of force and displacement: W = F ⋅ d.

Applications in Physics:
- Mechanics: Dot product finds applications in mechanics to calculate work, torque, and energy.
- Electromagnetism: In electromagnetism, it is used to find the electric and magnetic flux through surfaces.
- Optics: Dot product is employed in optics to calculate the intensity of light and polarisation.
- Quantum Mechanics: In quantum mechanics, it is used to calculate probabilities and expectation values of observables.
- Fluid Mechanics: Dot product helps in computing the dot product of velocity and force fields, aiding in the analysis of fluid flow.
In conclusion, the dot product of vectors is a versatile mathematical operation with wide-ranging applications in physics and engineering. Its simplicity belies its importance in describing and analysing various physical phenomena, making it an indispensable tool in the physicist’s toolkit.